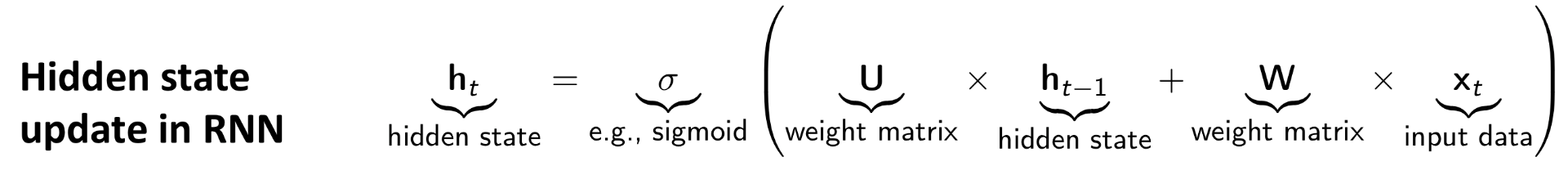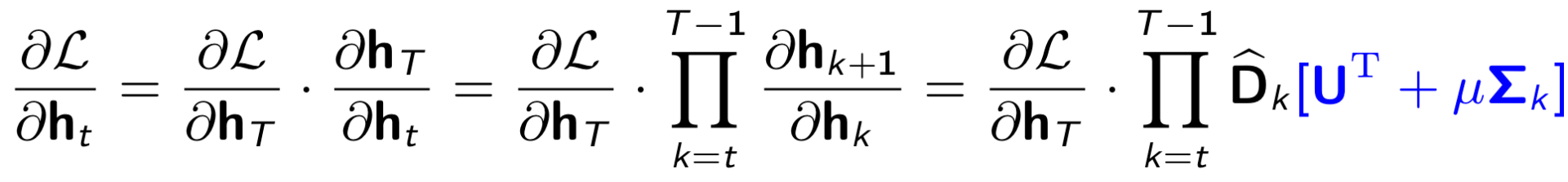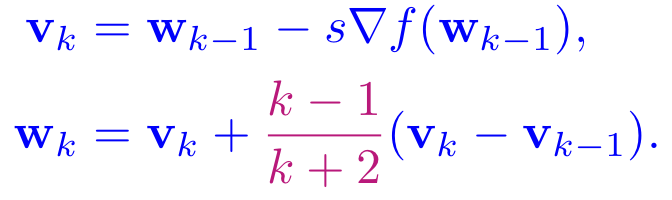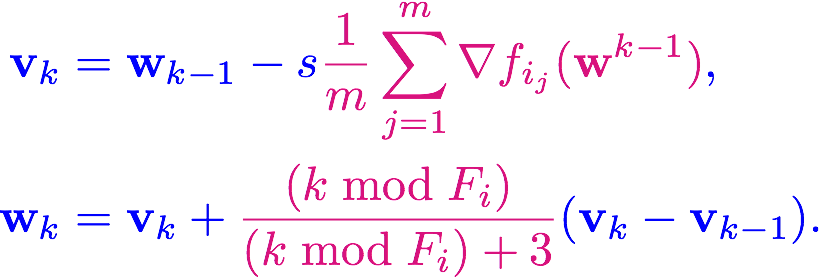What is MomentumRNN about?
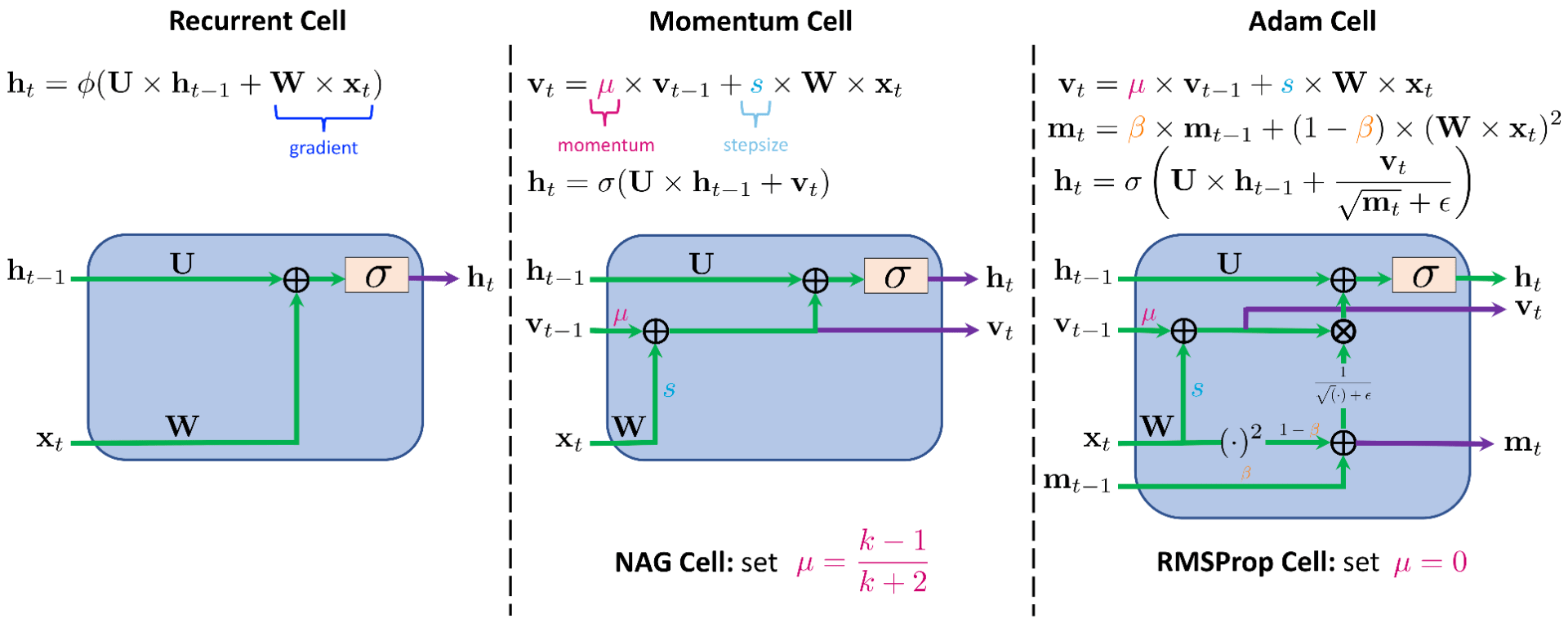
We develop a gradient descent (GD) analogy of the recurrent cell. In particular, the hidden state update in a recurrent cell is associated with a gradient descent step towards the optimal representation of the hidden state. We then integrate momentum that used for accelerating gradient dynamics into the recurrent cell, which results in the momentum cell as shown in Figure 1. At the core of the momentum cell is the use of momentum to accelerate the hidden state learning in RNNs. We call the RNN that consists of momentum cells the MomentumRNN [1].
Here are our research paper, slides, lighting talk, and code.
Figure 1: Comparison between the momentum-based cells and the recurrent cell.
Why does MomentumRNN matter?
The major advantages of MomentumRNN are fourfold:
- MomentumRNN can alleviate the vanishing gradient problem in training RNN.
- MomentumRNN accelerates training and improves the accuracy of the baseline RNN.
- MomentumRNN is universally applicable to many existing RNNs.
- The design principle of MomentumRNN can be generalized to other advanced momentum-based optimization methods, including Adam [2] and Nesterov accelerated gradients with a restart [3, 4].
Why does MomentumRNN have a principled approach?
First, let us review the hidden state update in RNN as given in the following equation.
In order to incorporate momentum into an RNN, we first interpret that the input data at time t provides a gradient for updating the hidden state at time t – 1. In particular, let us consider the following re-parameterization of the hidden state update equation.
The recurrent cell can then be re-written as:
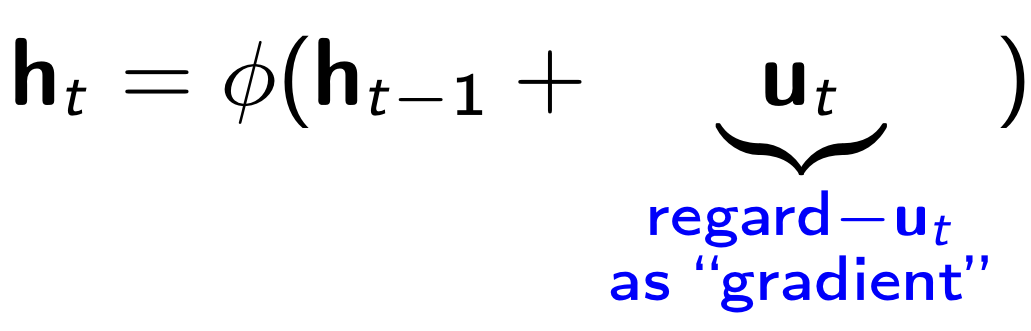 Adding momentum to the recurrent cell yields
Adding momentum to the recurrent cell yields
Let![]() We get the following momentum cell
We get the following momentum cell
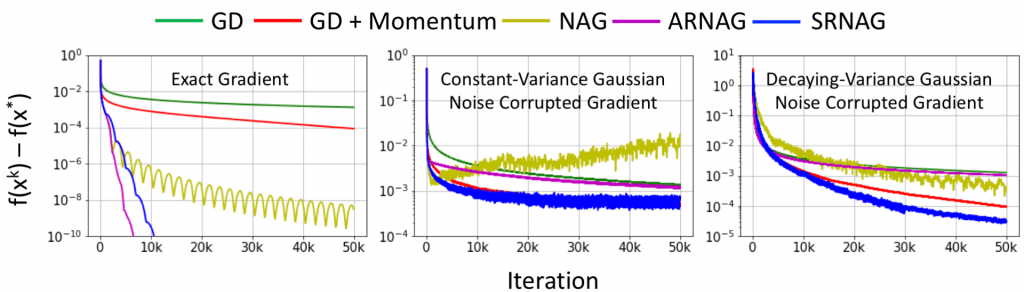
Momentum cell is derived from the momentum update for gradient descent, and thus, it is principled with theoretical guarantees provided by the momentum-accelerated dynamical system for optimization. Similar derivation can be employed to derive other momentum-based cells from state-of-the-art optimization methods, such as the Adam cell, the RMSProp cell, and the Nesterov accelerated gradient cells as illustrated in Figure 1.
Furthermore, applying backpropagation-through-time on the MomentumRNN, we can show that
According to the above equation, choosing a proper momentum constant μ in MomentumRNN helps alleviate the vanishing gradient problem.
Why is MomentumRNN simple?
Implementing momentum cells only requires changes in a few lines of the recurrent cell code. Also, our momentum-based principled approach can be integrated into LSTM and other RNN models easily.
Does MomentumRNN work?
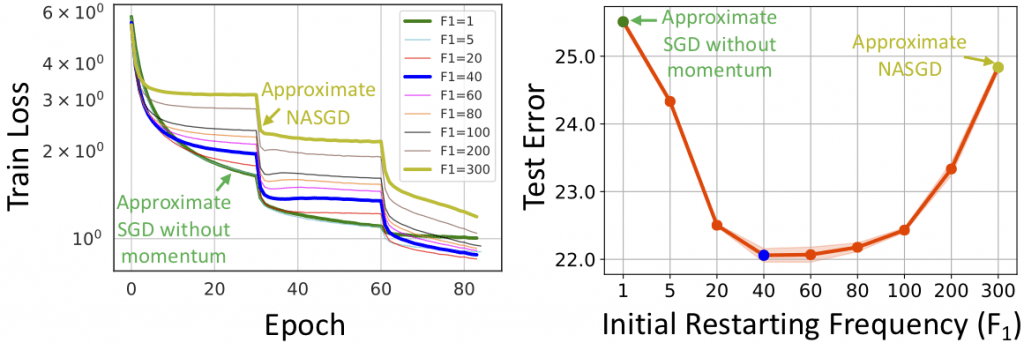
1. Our momentum-based RNNs outperform the baseline RNNs on a variety of tasks across different data modalities. Below we show our empirical results on (P)MNIST and TIMIT tasks. Results for other tasks can be found in our paper.
Figure 2: Momentum-based LSTMs outperform the baseline LSTMs on (P)MNIST image classification and TIMIT speech recognition tasks.
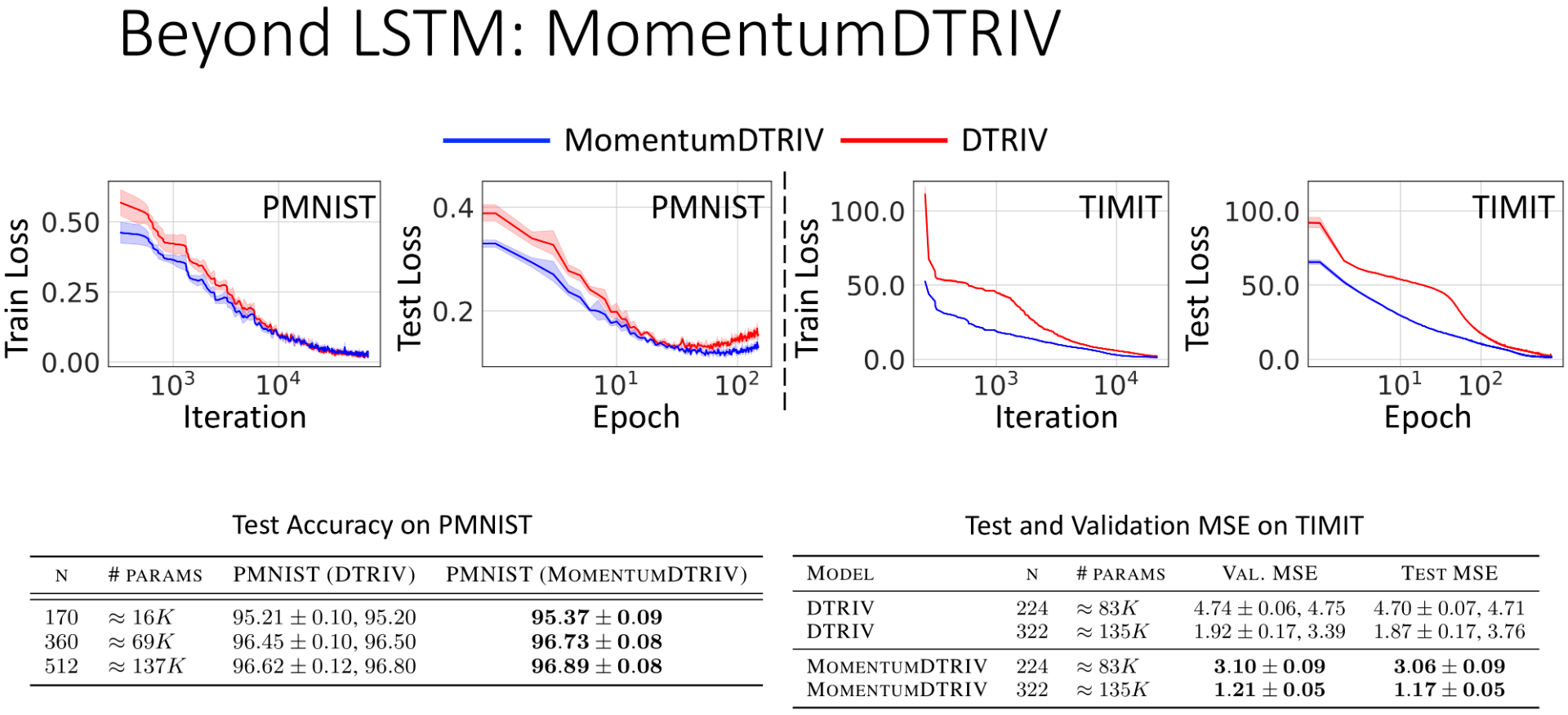
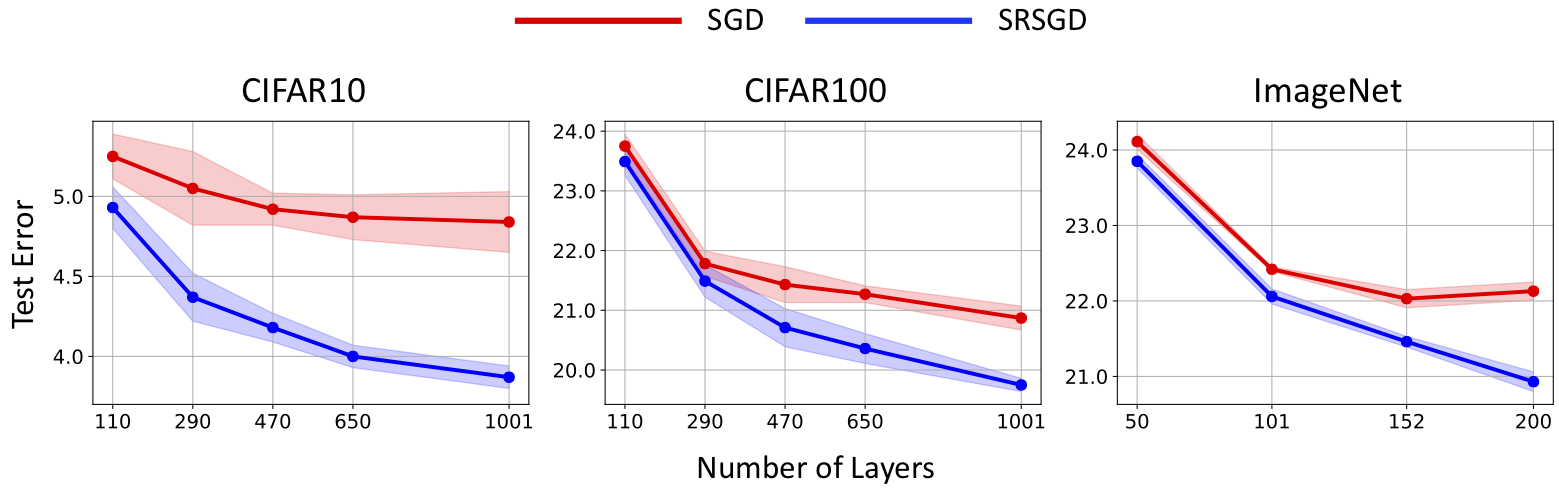
2. Our momentum-based approach can be applied to the state-of-the-art RNNs to improve their performance. Below we consider the orthogonal RNN equipped with dynamic trivialization (DTRIV) as a baseline and show that our MomentumDTRIV still outperforms the baseline DTRIV on PMNIST and TIMIT tasks.
Figure 3: Our momentum approach helps improve the performance of the state-of-the-art orthogonal RNN equipped with dynamic trivialization (DTRIV).
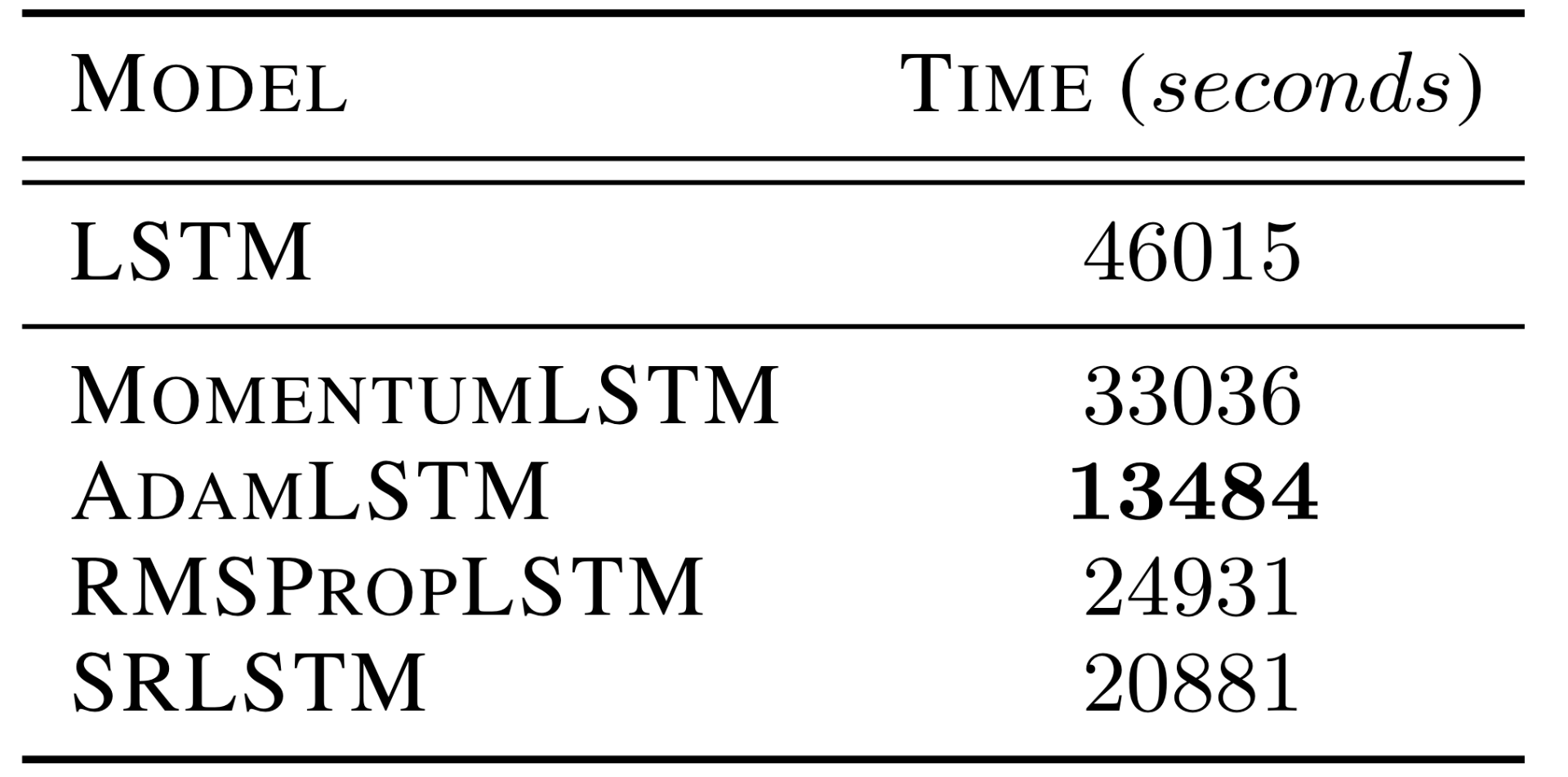
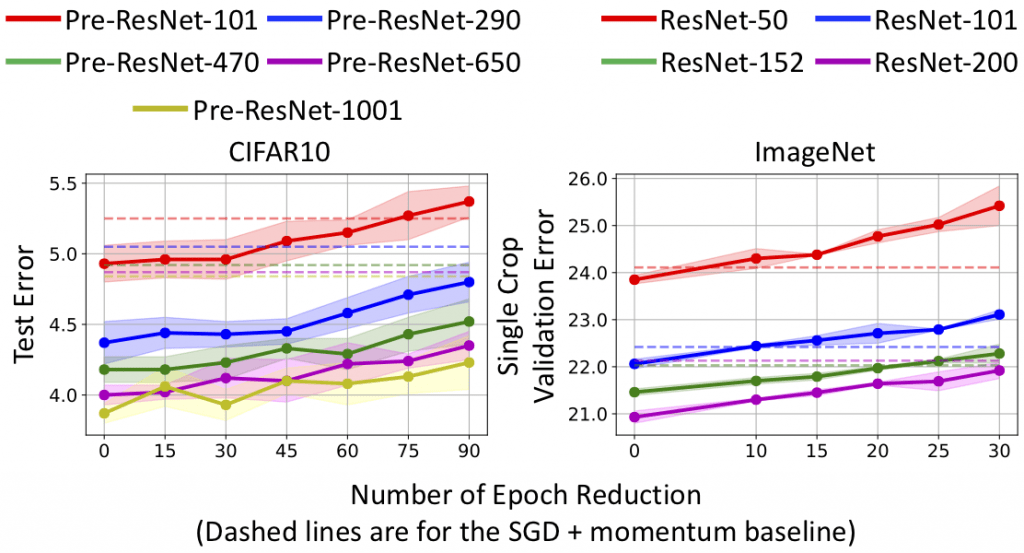
3. Momentum-based RNNs are much more efficient than the baseline RNNs. Figure 4 shows that momentum-based RNNs require much less time to reach the same test accuracy as the corresponding RNNs.
Figure 4: Total computation time to reach the same 92.29% test accuracy of LSTM for PMNIST classification task.
References
1. Tan Nguyen, Richard G Baraniuk, Andrea L Bertozzi, Stanley J Osher, and Bao Wang. MomentumRNN: Integrating Momentum into Recurrent Neural Networks. In Advances in Neural Information Processing Systems, 2020.
2. Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
3. Yurii E Nesterov. A method for solving the convex programming problem with convergence rate o (1/kˆ 2). In Dokl. Akad. Nauk Sssr, volume 269, pages 543–547, 1983.
4. Bao Wang, Tan M Nguyen, Andrea L Bertozzi, Richard G Baraniuk, and Stanley J Osher. Scheduled restart momentum for accelerated stochastic gradient descent. arXiv preprint arXiv:2002.10583, 2020.